ÁLGEBRA

Se conoce como álgebra a la rama de la matemática en la cual las operaciones son generalizadas empleando números, letras y signos que representan simbólicamente un número u otra entidad matemática.

Según Baldor, álgebra es la rama de la matemática que estudia la cantidad considerada del modo más general posible. En este sentido, se puede reseñar que la enseñanza del álgebra está dominada por la obra “Álgebra de Baldor”, libro del matemático cubano Aurelio Baldor, que desarrolla y trata de todas las hipótesis de esta ciencia.

Etimológicamente, la palabra álgebra es de origen árabe que significa “recomposición” o “reintegración”. El álgebra procede desde las civilizaciones de Babilonia y Egipto, antes de Cristo, usaban dicho método para resolver ecuaciones de primer y segundo grado.

OPERACIONES ARITMÉTICAS CON POLINOMIOS

Ahora que conocemos los distintos tipos de polinomios que existen en el álgebra, no está de más que tengamos en cuenta las operaciones con polinomios que podemos encontrar en nuestros ejercicios de matemáticas. Si ya somos capaces de identificar cómo se clasifican los diferentes tipos de polinomios, ahora toca descubrir la forma en que se realizan las diferentes operaciones con polinomios que existen. Para dar un paso adelante en esta parte tan interesante del álgebra, conoce qué debes hacer en cada momento, con las operaciones con polinomios resueltas que tienes a continuación.

SUMA

Cuando sumamos diferentes polinomios debemos sumar los coeficientes que tengan el mismo grado, es decir, que sólo podemos sumar coeficientes que tengan el mismo exponente. Por ello, es conveniente ordenar los números para que sea mucho más fácil realizar la suma.

 

 

 

RESTA 

La resta de polinomios se realiza mediante el mismo proceso que la suma de polinomios pero restando el sustraendo al minuendo, o lo que es lo mismo, sumando al primer polinomio el opuesto del segundo. Cabe recordar que hay que ir con cuidado con los signos, ya que cuando restamos un número negativo se convierte en una suma. Puedes verlo en estos ejemplos de operaciones con polinomios.

 

 

MULTIPLICACIÓN 

Existen diversas operaciones de multiplicaciones con polinomios:

Multiplicación de un número por un polinomio

Cuando multiplicamos un número natural por un polinomio se multiplica el número por cada una de la unidades de cada monomio, y se respeta el mismo exponente. De esta forma seguimos teniendo un polinomio del mismo grado.

 

Multiplicación de un monomio por un polinomio

En este tipo de operaciones debemos multiplicar el monomio por cada uno de los monomios que forman el siguiente polinomio. Cuando multiplicamos diferentes monomios debemos multiplicar las unidades que la forman y sumar los exponentes que poseen. Averigua cómo resolver estas operaciones con polinomios. Por ejemplo: 4x2 · 2x3 = 8x5

 

Multiplicación de polinomios

Para llevar a cabo esta operación debemos multiplicar cada uno de los monomios del primer polinomio, por todos los elementos del segundo polinomio. Después debemos sumar todos los monomios que posean el mismo coeficiente y obtendremos el polinomio resultante. Con estos ejemplos entenderás la explicación de las operaciones con polinomios.

 

DIVISIÓN DE POLINOMIOS

Para realizar la división debemos colocar a la izquierda el dividendo y a la derecha el divisor, tal y como se hacen las divisiones tradicionales. Para empezar hay que dividir el primer monomio del dividendo entre el primer monomio del divisor (8x3 : 2x2) y el resultado los ponemos como el primer número del cociente (4x). Después multiplicamos este número del cociente por el divisor y se lo restamos al dividendo. Estos ejercicios resueltos de división de polinomios te ayudarán a entender cómo se hacen.

 

 

 

PRODUCTOS NOTABLES

Los productos notables son simplemente multiplicaciones especiales entre expresiones algebraicas las cuales sobresalen de las demás multiplicaciones por su frecuente aparición en matemáticas. De ahí el nombre producto, que hace referencia a "multiplicación" y notable, que hace referencia a su "destacada" aparición.

Así bien, una vez aprendido dichos productos notables, no habrá necesidad de comprobar dicha multiplicación mecánicamente, es decir, solo debemos seguir las reglas aprendidas con anterioridad que caracterizan a cada producto notable. 

 

 

CASOS DE FACTORIZACIÓN 

CASO 1

EL PRIMER CASO DE FACTORES SE DIVIDE EN DOS PARTES QUE SON: FACTOR COMÚN MONOMIO Y FACTOR COMÚN POLINOMIO
FACTOR COMÚN MONOMIO

Es una expresión algebraica en la que se utilizan exponentes naturales de variables literales que constan de un solo término si hubiera + ó – seria binomio, un número llamado coeficiente. Las únicas operaciones que aparecen entre las letras son el producto y la potencia de exponentes naturales. Se denomina polinomio a la suma de varios monomios. Un monomio es una clase de polinomio con un único término.

EJEMPLO 1:

5a2 - 15ab - 10 ac
El factor común entre los coeficientes es 5 y entre los factores literales es a, por lo tanto
 5a2 - 15ab - 10 ac = 5a·a - 5a·3b - 5a · 2c = 5a(a - 3b - 2c)

CASO 2

FACTOR COMUN POR AGRUPACION

Se llama factor común por agrupación de términos, si los términos de un polinomio pueden reunirse en grupos de términos con un factor común diferente en cada grupo.
Cuando pueden reunirse en grupos de igual número de términos se le saca en cada uno de ellos el factor común. Si queda la misma expresión en cada uno de los grupos entre paréntesis, se la saca este grupo como factor común, quedando así una multiplicación de polinomios.
Tratar desde el principio que nos queden iguales los términos de los paréntesis nos hará más sencillo el resolver estos problemas.

EJEMPLO1

2ax + 2bx - ay + 5a - by + 5b
Agrupo los términos que tienen un factor común:
                        (2ax - ay + 5a) + (2bx - by + 5b)
Saco el factor común de cada grupo:
                        a (2x - y + 5 ) + b (2x - y + 5 )
Como las expresiones encerradas entre paréntesis son iguales se tiene:
                        (2x -y +5)(a + b)

CASO 3

TRINOMIO CUADRADO PERFECTO
Es igual al cuadrado de un binomio. Se llama trinomio cuadrado perfecto al trinomio (polinomio de tres términos) tal que, dos de sus términos son cuadrados perfectos y el otro término es el doble producto de las bases de esos cuadrados.

EJEMPLO  1 :

a2 +2ab + b2= (a+b)2
4x2 – 20xy + 25y2= (2x – 5y) (2x – 5y) = (2x – 5y)2 R/.
16 + 40x2 + 25x4 = (4 + 5x2) (4 + 5x2) = (4 + 5x2)2
9b2 – 30a2b + 25a4 = (3b – 5a2) (3b – 5a2) = (3b – 5a2)2
400x10 + 40x5 + 1 = (20 x5 + 1) (20 x5 + 1) = (20 x5 + 1)2

CASO 4

DIFERENCIA DE CUADRADOS

Se identifica por tener dos términos elevados al cuadrado y unidos por el signo menos. Se resuelve por medio de dos paréntesis, (parecido a los productos de la forma), uno positivo y otro negativo. En los paréntesis deben colocarse las raíces.

EJEMPLO  1:

1  9y2-4x2= (3y-2x) (3y+2x)   R//

CASO ESPECIAL

La regla empleada en los ejemplos anteriores es aplicable a las diferencias de cuadrado en que uno o ambos cuadrados son expresiones compuestas.
Así, en este caso, tenemos: La raíz cuadrada de (a + b)2 es (a + b) La raíz cuadrada de c2 es  c  
Multiplica la suma de las raíces, (a + b + c) por la diferencia entre la raíz del minuendo y la del Sustraendo (a + b - c)

EJEMPLO  1:

1   4x2 - (x + y)2

4x2 - (x + y)2 = [2x + (x + y)] * [2x - (x + y)]
4x2 - (x + y)2 = [2x + x + y] * [2x - x - y]
4x2 - (x + y)2 = [3x + y] * [x - y]

CASO 5

TRINOMIO CUADRADO PERFECTO POR ADICION Y SUSTRACCION
Algunos trinomios no cumplen las condiciones para ser trinomios cuadrados perfectos, el primer y tercer término tienen raíz cuadrada perfecta pero el de la mitad no es el doble producto de las dos raíces. Se debe saber cuanto debe ser el doble producto y la cantidad que falte para cuadrar el término de la mitad, esta cantidad se le suma y se le resta al mismo tiempo, de tal forma se armara un trinomio cuadrado y factorizado unido con el último término tendremos una diferencia de cuadrados.

  EJEMPLOS 1

   4a4 + 8a2 b2 + 9b4
4a4 + 8a2 b2 + 9b4
      + 4a2 b2             - 4a2 b2
4a4 +12a2b2 + 9b4- 4a2b2 = (4a4 + 12a2 b2 + 9b4) - 4a2b2

 (4a4 + 12a2 b2 + 9b4) - 4a2 b2
 (2a2 + 3b2)2 - 4a2 b2
(2a2 + 3b2)2 - 4a2 b2 = [(2a2 + 3b2) + 2ab] * [(2a2 + 3b2) - 2ab]
(2a2 + 3b2)2 - 4a2 b2 = [2a2 + 3b2 + 2ab] * [2a2 + 3b2 - 2ab]
4a4 + 8a2 b2 + 9b4= [2a2 + 2ab + 3b2] * [2a2 – 2ab + 3b2]

CASO 6

TRINOMIO DE LA FORMA x2 + bx + c

Trinomios de la forma x2 + bx + c son trinomios como

x2 + 5x + 6
a2 – 2a – 15
m2 + 5m – 14
y2 – 8y + 15

Que cumplen las condiciones siguientes:
• El coeficiente del primer término es 1
• El primer término es una letra cualquiera elevada al cuadrado.
• El segundo término tiene la misma letra que el primero con exponente 1 y su coeficiente es una cantidad cualquiera, positiva o negativa.
• El tercer termino es independiente de la letra que aparece en el primer y segundo termino y es una cantidad cualquiera, positiva o negativa

EJEMPLO  1

x2 + 5x + 6 = (x + 2) * (x + 3)

           CASO ESPECIAL DEL CASO 6

El procedimiento anterior es aplicable a la factorización de trinomio que siendo de la forma x2+bx+c difieren algo de los estudiados anteriormente.
Ejemplo:
X4-5x2-50 =
El primer término de cada factor binomio será la raíz cuadrada de X4 o sea X2
X4-5x2-50 = (X2 -  ) (X2 +  )
Buscamos dos números cuya diferencia (signos distintos en los binomios) sea 5 y cuyo producto sea 50. Esos números son 10 y 5 tendremos:
X4-5x2-50 = (X2 - 10) (X2 + 5)

EJEMPLOS 1
c2 + 5c – 24 =
c2 + 5c – 24 = (c + 8) * (c – 3)
 

CASO 7

TRINOMIO DE LA FORMA AX2+BX+C
Condiciones que debe cumplir un trinomio de la forma ax2+bx+c:
El primer término tiene un coeficiente mayor que 1 y tiene una letra cualquiera elevada al cuadrado.
El segundo término tiene la misma letra que el primero pero con exponente 1 y su coeficiente es una cantidad cualquiera positiva o negativa.
El tercer término es una cantidad cualquiera positiva o negativa sin ninguna letra en común con el 1 y 2 términos.

Ejemplo  1 :
6x2 -7x -3
1) Se multiplica el coeficiente del primer término” 6” por todo el trinomio, dejando el producto del 2  término indicado:
6(6x2 -7x +3) =36x2 -6(7x) -18
2) Se ordena tomando en cuenta que 36x2 = (6x)2 y 6(-7x) = -7(6x), escribiéndolo de la siguiente manera: (6x) 2 -7(6x) -18
3) Luego se procede a factorar (6x) 2 -7(6x) -18 como un problema del Caso VI. Con una variante que se explica en el Inciso 6°
4) Se forman 2 factores binomios con la raíz cuadrada del primer término del trinomio: (6x-  )(6x+  )
5) Se buscan dos números cuya diferencia sea -7  y cuyo producto sea -18 esos números son -9 y +2  porque: -9 +2 = -7  y (-9) (2) = -18= (6x-9)(6x+2)
6) Aquí está la variante: Como al principio multiplicamos el trinomio por “6″, entonces ahora los factores binomios encontrados, los dividimos entre”6″
(6x-9)(6x+2) / 6; como ninguno de los binomios es divisible entre “6″ entonces descomponemos el “6″ en dos factores (3y2), de manera que uno divida a un factor binomio y el segundo divida al otro. Así: (6x-9) / 3 y (6x+2) / 2, y estos cocientes quedarían así:(2x-3) (3x+1)

CASOS ESPECIALES
EJEMPLO    1 :

20x^2 +7x -6 = (4x+3) (5x-2)
3x² + 8x – 35 = (3x - 7) (x + 5)
8. 9a² + 9ab - 18b² = (a + 2b) (a - b)
9. 4x² +17x -15 = (4x - 3) (x + 5)
10. 15x² + x - 2 = (5x + 2) (3x - 1)

CASO 8

CUBO PERFECTO DE BINOMIOS
Debemos tener en cuenta que los productos notables nos dicen que:
(a+b)3 = a2 +3a 2 b+3 a b 2 +b3 y (a-b)3 = a2-3a 2 b+3ab 2 - b3
La fórmula de arriba nos dice que para una expresión algebraica ordenada con respecto a una parte literal sea el cubo de un binomio, tiene que cumplir lo siguiente:
1. Tener cuatro términos.
2. Que el primer término y el último sean cubos perfectos.
3. Que el segundo término sea más o menos el triplo de la primera raíz cúbica elevada al cuadrado que multiplica la raíz cúbica del último término.
4. Que el tercer término sea el triplo de la primera raíz cúbica por la raíz cubica del último término elevada al cuadrado
Si todos los términos de la expresión algebraica son positivos, la respuesta de la expresión dada será la suma de sus raíces cúbicas de su primer y último término, y si los términos son positivos y negativos la expresión será la diferencia de dichas raíces.

EJEMPLO   1
1) 8a3 -36a2b+54ab2-27b3
La raíz cúbica de 8a3 es 2a
La raíz cúbica de 27b3es 3b
3(2 a)2(3b) = 36a2 b, segundo término
3(2 a) (3b)2 = 54ab2, tercer término
Y como los términos son alternativamente positivos y negativo, la expresión dada es el cubo de:
R. (2a -3b)3
 

CASO 9

SUMA O DIFERENCIA DE CUBOS PERFECTOS

Pasos para resolver el ejercicio:
1. Descomponemos en dos factores.
2. En el primer factor se escribe la suma o la diferencia según sea el caso, de las raíces cúbicas de los dos términos.
3. En el segundo factor se escribe la raíz del primer termino elevada al cuadrado, empezando con el signo menos y de ahí en adelante sus signos alternados (si es una suma de cubos) o con signo más (si es una diferencia de cubos) el producto de la primera raíz por la segunda, más el cuadrado de la segunda raíz.
La fórmula (1) nos dice:
REGLA 1 la suma de dos cubos perfectos se descompone en dos factores:
1. La suma de sus raíces cúbicas
2. El cuadrado de la primera raíz, menos la multiplicación de las dos raíces, más el cuadrado de la segunda raíz. a3 +b3 =(a+b) (a2-ab+b2)
La fórmula (2) nos dice:
REGLA 2
La diferencia de dos cubos perfectos se descompone en dos factores:
1. La diferencia de sus raíces cúbicas
2. El cuadrado de la primera raíz, más el cuadrado de la segunda raíz.
a3 - b3 =(a-b) (a2+ab+b2)

EJEMPLO 1
27x3 + 125 y9 = (3x+5y3) (9x2-15x y3+25y6)
1 – a3 = (1-a) (1+a+ a2)
1 + a3 = (1+a) (1-a+ a2)
a3 + 27 = (a+3) (a2- 3a+ 9)
x3 – 27 = (x -3) (x2- 3x+ 9)

CASO 10

SUMA O DIFERENCIA DE DOS POTENCIAS IGUALES

Procedimiento:
Se aplican los siguientes criterios:
Criterios de divisibilidad de expresiones de la forma an + - bn

Criterio 1: an – bn  es divisible por a - b siendo n par o impar
Criterio 2: an – bn  es divisible por a + b siendo n impar
Criterio 3: an – bn  es divisible por a + b siendo n es par
Criterio 4: an + bn  nunca es divisible por a - b

Pasos para resolver la suma de dos potencias iguales
Factorar x5 +32
1.- Encontramos la raíz quinta de los términos:
Raíz quinta de x5 = x; raíz quinta de 32 = 2
2.- Formamos el primer factor con las raíces: (x +2)
3.- Formamos el segundo factor:

(x4 – x3(2) +x2(2)2 – x (2)3 + (2)4) = (x4 – 2x3 + 4x2 – 8x + 16)
 x5 +32 = (x +2) (x4 – 2x3 + 4x2 – 8x + 16)

EJEMPLO   1 :

1.) x7+128
1.- Encontramos la raíz séptima de los términos:
Raíz séptima de x7 = x; raíz séptima de 128 = 2   

ECUACIONES DE PRIMER GRADO Y SEGUNDO GRADO

Uno de los conceptos más sencillos y útiles de entender en el cálculo es aprender a calcular las ecuaciones de primer y segundo grado. Estas son las dos principales ecuaciones que forman la base de todas las demás ecuaciones que involucran números complejos, como la ecuación cúbica, cuadrática, la hipérbola y la parábola. Aunque puede ser bastante difícil para un estudiante entender estas ecuaciones, es importante recordar que forman la base de casi todos los cursos avanzados de matemáticas en el cálculo. Por lo tanto, es importante dominar las técnicas para resolver problemas en esta área.

Una ecuación de primer grado es una ecuación cuya solución viene dada por Primero, el producto de sus variables (en este caso, x), y el valor medio de sus fórmulas integrales, como la matriz integral. Una ecuación de segundo grado es lo contrario de su homóloga de primer grado. Así, una solución de una ecuación de primer grado será siempre la suma de sus variables, mientras que las soluciones de una ecuación de segundo grado serán siempre iguales a los valores de primer grado de sus correspondientes variables. Además, las soluciones de las ecuaciones de tercer grado también son iguales a los valores de sus correspondientes variables, pero esto ocurre raramente.

En general para resolver una ecuación de primer grado debemos seguir los siguientes pasos:

1 Quitar paréntesis.

 

2 Quitar denominadores.

 

3 Agrupar los términos en {x} en un miembro y los términos independientes en el otro.

 

4 Reducir los términos semejantes.

 

5 Despejar la incógnita.

 

SISTEMAS CON ECUACIONES CON DOS INCOGNITAS

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas en la que deseamos encontrar una solución común. En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas. Una ecuación lineal con dos incógnitas es una igualdad del tipo ax+by=c, donde a, b, y c son números, y «x» e «y» son las incógnitas. Una solución es todo par de números que cumple la ecuación. Los sistemas de ecuaciones lineales los podemos clasificar según su número de soluciones:
 

Compatible determinado: Tiene una única solución, la representación son dos rectas que se cortan en un punto.

Compatible indeterminado: Tiene infinitas soluciones, la representación son dos rectas que coinciden.

Incompatible: No tiene solución, la representación son dos rectas paralelas.
 

Existen diferentes métodos de resolución:

    Sustitución.
     Reducción.
     Igualación.

En esta ocasión vamos a resolver un sistema de dos ecuaciones lineales con dos incógnitas. Por ejemplo:

Sistema de ecuaciones: método de sustitución

A través del método de sustitución lo que debemos hacer es despejar una de las incógnitas en una de las ecuaciones y sustituir su valor en la siguiente. Lo veremos con más detalle en el siguiente ejemplo:

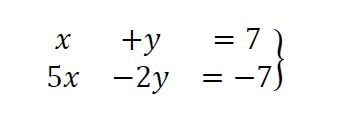
Lo primero que hacemos es despejamos una de las incógnitas en la primera ecuación.

x+y=7
x= 7-y

Posteriormente, sustituimos en la segunda ecuación el valor correspondiente de la «x».

5x-2y=-7
5.(7-y)-2y=-7

Ahora, despejamos la «y».

35-5y-2y=-7
35-7y=-7
-7y=-7-35
-7y=-42
y=-42/-7=6

y=6

Por último, utilizamos el valor de «y» para hallar el valor de «x».

x= 7-y

x=7-6=1

x=1

La solución de nuestro sistema es x=1 e y =6.

Sistema de ecuaciones: método de reducción

Con el método de reducción lo que hacemos es combinar, sumando o restando, nuestras ecuaciones para que desaparezca una de nuestras incógnitas.

Los pasos a seguir son los siguientes: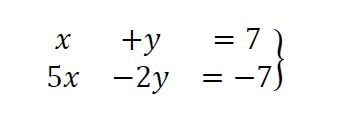


En primer lugar, necesitamos preparar las dos ecuaciones, si es necesario, multiplicándolas por los números que convenga.

En este caso, queremos reducir la «y» de nuestro sistema, por tanto, multiplicamos la primera ecuación por 2.

2(x+y=7)
5x-2y=-7

Así, el sistema se queda:

Si nos fijamos, sumando las ecuaciones la y nos desaparece.

Y nos quedaría:

7x=7
x=7/7=1
x=1

Por último, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.

y= 7-x

y=7-1=6

y=6

La solución de nuestro sistema es x=1 e y =6.

Sistema de ecuaciones: método de igualación

El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones y después igualar los resultados.

Los pasos a seguir son los siguientes:

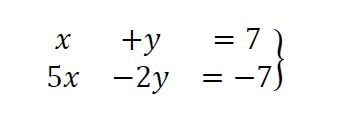
En primer lugar, elegimos la incógnita que deseamos despejar. En este caso, empezaré por la «x» y despejo la misma en ambas ecuaciones.

x+y=7; x=7-y

5x-2y=-7; 5x=2y-7; x=(2y-7)/5

Una vez hemos despejado, igualamos:

7-y=(2y-7)/5
5(7-y=(2y-7)/5)
35-5y=2y-7
42=7y
y=42/7=6

y=6

Por último, sustituimos el valor que hemos calculado despejando la otra incógnita en una de las ecuaciones iniciales.

x=7-y
x=7-6=1

x=1

La solución de nuestro sistema es x=1 e y =6.

SISTEMAS DE ECUACIONES CON TRES INCOGNITAS

Para resolver un sistema de tres ecuaciones con tres variables, puedes utilizar uno de varios métodos. Aquí tienes dos enfoques comunes:

    Eliminación gaussiana: Este método consiste en sumar o restar ecuaciones para eliminar variables, de una en una, hasta que el sistema se encuentre en lo que se conoce como forma reducida fila-echelón. Una vez que el sistema está en esta forma, es fácil resolver las variables.
    Regla de Cramer: Este método consiste en expresar la solución en términos de determinantes de determinadas matrices. Para utilizar la regla de Cramer, es necesario poder calcular determinantes, lo que puede resultar un poco más complicado que los métodos utilizados en la eliminación de Gauss.

He aquí un ejemplo de cómo resolver un sistema de tres ecuaciones con tres variables utilizando la eliminación de Gauss:

Supongamos que tenemos el siguiente sistema:

{3x+4y–2z=02x–3y+4z=11x–2y+3z=7
⎩
⎨

⎧​3x+4y–2z=02x–3y+4z=11x–2y+3z=7​

Podemos empezar eliminando la variable x de la segunda y tercera ecuaciones. Para ello, multiplicamos la segunda ecuación por 1 y la tercera ecuación por -2, y luego sumamos las ecuaciones resultantes:

{2x–3y+4z=11−2x+4y−6z=−14
{2x–3y+4z=11−2x+4y−6z=−14​

____________________

y−2z=−3y−2z=−3

Luego, podemos eliminar la variable x de las ecuaciones primera y tercera, multiplicando la primera ecuación por 1 y la tercera ecuación por -3, y sumando después las ecuaciones resultantes:

{3x+4y−2z=0−3x+6y−9z=−21
{3x+4y−2z=0−3x+6y−9z=−21​

____________________

10y−11z=−2110y−11z=−21

Por último, podemos multiplicar a la ecuación y−2z=−3y−2z=−3 por -10 y sumar estas dos ecuaciones para eliminar la variable y:

{−10y+20z=3010y−11z=−21
{−10y+20z=3010y−11z=−21​

____________________

9z=99z=9

Resolviendo esta ecuación para z, encontramos que z=1z=1.

Sustituyendo este valor en la ecuación y−2z=−3y−2z=−3, podemos resolver para y: y=−1y=−1.

Sustituyendo estos valores de nuevo en las ecuaciones originales, podemos resolver para x: x=2x=2.

Por lo tanto, la solución del sistema es x=2x=2, y=−1y=−1 y z=1z=1. 

INTERVALOS

Un intervalo es un conjunto de números reales que se encuentra comprendido entre dos extremos, a y b. También puede llamarse subconjunto de la recta real. Por ejemplo, los números que satisfagan una condición 1 ≤ x ≤ 5 ó [1;5] implican un intervalo que va desde el 1 hasta el 5, incluyendo a ambos. Si se toma en cuenta la aplicación del intervalo para observar el comportamiento de una variable, se toma una serie de tiempo y se escoge un intervalo.

CLASIFICACIÓN DE INTERVALOS

Existen 4 tipos de intervalos matemáticos, estos son: abierto, cerrado, semiabierto e infinito.

Intervalo abierto

Un intervalo abierto es aquel que no incluye los extremos entre los cuales está comprendido, pero sí todos los valores ubicados entre estos. Se representa mediante una expresión del tipo a < x < b ó (a;b).

Por ejemplo, si tenemos el intervalo abierto (1;5), tendremos el conjunto de números mayores a 1 y menores que 5. Sin incluir el 1 y el 5.

 

Intervalo cerrado

Un intervalo cerrado es aquel que incluye los extremos del intervalo y todos los valores comprendidos entre estos. Se representa con una expresión del tipo a ≤ x ≤ b ó [a;b].

Por ejemplo, si tenemos el intervalo cerrado [1;5], tendremos el conjunto de números mayores o iguales a 1 y menores o iguales a 5. Incluyendo el 1 y el 5.
Representación de un intervalo cerrado.

 

 

Intervalo semiabierto

Un intervalo semiabierto es aquel que incluye tan solo uno de los extremos de los valores que están entre ellos, de modo que el otro extremo queda excluido. Pueden estar incluidos o excluidos tanto el extremo derecho como el izquierdo.

Se representa con una expresión del tipo a ≤ x < b ó a < x ≤ b, lo que sería [a;b) ó (a;b].

Por ejemplo, si tenemos el intervalo semiabierto [1;5), tendremos un conjunto de números mayores o iguales a 1 y menores a 5. Incluyendo el 1 pero no el 5.
Representación de un intervalo semiabierto.

 

 

Intervalo infinito

Un intervalo infinito es aquel que tiene un valor infinito en uno o ambos extremos. El extremo que posea el infinito será un extremo abierto. En caso de que ambos extremos sean infinitos, será la recta real.

Se representa con una expresión del tipo a ≤ x ó x ≤ a, lo que sería [a;∞) ó (-∞;a). Estos además pueden contener intervalos cerrados, como [a; ∞).

Por ejemplo, si tenemos el intervalo infinito [1;∞), tendremos un conjunto de números mayores o iguales a 1 en adelante.

 

OPERACIONES CON INTERVALOS

Los intervalos son conjuntos de números reales que se pueden representar gráficamente sobre la recta real. Se pueden trabajar con las reglas de los conjuntos en general, como son el complemento, la intersección, la unión, la diferencia y la diferencia simétrica. La comprensión de los intervalos permite el trabajo con el dominio y el rango de relaciones y funciones.

Para tener un manejo adecuado del trabajo con intervalos, es necesario graficarlos en la recta real y escribirlos en la notación de conjuntos a partir de desigualdades. De otro lado, la ubicación de puntos en el plano y sombreado de regiones en el mismo son aspectos que se deben de tener en cuenta cuando se trabaja con desigualdades.Los intervalos son conjuntos de números reales, por lo tanto, se pueden realizar las operaciones definidas entre conjuntos: unión, intersección, diferencia, diferencia simétrica y complemento.

Para los conjuntos definidos como intervalos, el conjunto universal o de referencia U es el conjunto de los números reales R. Cualquier subintervalo se denota por una letra mayúscula. Si A está contenido en los números reales, gráficamente, se puede representar de la siguiente manera:

 

 

UNION E INTERSECCION

 UNION

La unión de dos intervalos A y B es el conjunto de todos los números que están en el intervalo A o bien están en el intervalo B o bien están en los dos intervalos a la vez.

Se representa con el símbolo ∪. Por ejemplo, la unión de dos intervalos se puede representar así:

Cómo calcular la unión de dos intervalos

Vamos a ver ahora cómo calcular la unión de dos intervalos al mimos tiempo que resolvemos unos ejemplos.

Empezamos por el primero:

En primer lugar, representamos el primer intervalo (-5,0] en la recta numérica. El primer intervalo comienza en -5, abierto por la izquierda, luego se representa un punto vacío y termina en 0, cerrado por la derecha, por lo que se representa con un punto lleno:

Ahora, en la misma recta, representamos el segundo intervalo (-1,∞), que comienza en -1 con un punto vacío ya que está abierto por la izquierda y termina es infinito, que siempre es un intervalo abierto y por tanto no se incluye en el intervalo:

La unión de estos dos intervalos corresponde con la parte de la recta que se queda coloreada, bien del primer intervalo (rojo), bien del segundo intervalo (azul) o por los dos intervalos (rojo y azul).

La parte coloreada de algún color empieza en -5 con un punto vacío, por lo que será abierto por la izquierda y termina en infinito, que al ser infinito queda abierto por la derecha:

Nota: Date cuenta que el -1, está vacío por el segundo intervalo, pero queda relleno por el primer intervalo, y por tanto pertenece a la unión.

Vamos a ver otro ejemplo de unión de intervalos:

Representamos el primer intervalo [-1,3) en la recta numérica: Está cerrado por la derecha, por lo que ponemos un punto lleno en -1 y abierto por la izquierda, por lo que en -3 corresponde un punto vacío:

Representamos el segundo intervalo (2,4) en la misma recta. Es un intervalo abierto, por lo que empieza en 2 con un punto vacío y termina en 4 con otro punto vacío:

La unión de los dos intervalos es la parte de la recta que se queda coloreada de algún color (o de ambos). En este caso empieza en -1 con un punto lleno y termina en 4 con un punto vacío, por tanto, el intervalo será cerrado por la izquierda y abierto por la derecha:

Unión de intervalos separados

Hay casos donde los intervalos están separados en la recta real, como por ejemplo el siguiente:

Si representamos ambos intervalos en la recta numérica nos queda: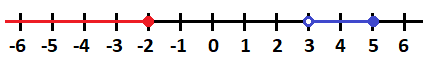

En este caso, la unión de intervalos no puede expresarse en un sólo intervalo, por lo que sigue siendo la unión de dos intervalos y no puede expresarse de otra forma:

INTERSECCIÓN

La intersección de dos intervalos A y B es el conjunto de todos los números que es común en el intervalo A y en el intervalo B.

Se representa con el símbolo ∩. Por ejemplo, la intersección de dos intervalos se puede representar así:

                

Cómo calcular la intersección de dos intervalos

Para calcular la intersección de dos intervalos, primero representamos ambos en la misma recta numérica y una vez representados, la  intersección de intervalos corresponderá con la parte de la recta en la que coinciden los dos intervalos.

Por ejemplo, vamos a calcular la intersección de los siguientes intervalos:

Representamos el primer intervalo (-4,3] en la recta, que comienza en -4 con un punto vacío y termina en 3 con un punto lleno, ya que está abierto por la izquierda y cerrado por al derecha: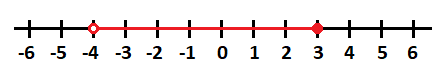

En la misma recta representamos el segundo intervalo (0,2], que comienza en 0 con un punto vacío y termina en 2 con un punto lleno, al estar abierto por la izquierda y cerrado por al derecha:

La parte donde coinciden ambos intervalos, es decir, que primero hemos pintado de rojo y después de azul, será la intersección de los intervalos. Es decir, es la parte donde coinciden los dos colores.

En nuestro caso, el tramo donde coinciden los dos intervalos empieza en 0 y termina en 2. El 0 está coloreado por el primer intervalo, pero tiene un punto vacío por el segundo intervalo, luego no es común a los dos intervalos y por tanto se queda fuera de la intersección, por lo que lo dejamos abierto por la izquierda.

El 2 está coloreado por el primer intervalo y tiene un punto lleno por el segundo intervalo, luego es común a ambos intervalos y por tanto, lo incluimos en la intersección cerrándolo con un corchete por la derecha.

Por tanto, la intersección de intervalos es:

Vamos a ver otro ejemplo:

Representamos el primer intervalo [-2,2), que empieza en -2 con un punto lleno y termina en 2 con un punto vacío, al ser un intervalo cerrado por la derecha y abierto por la izquierda:

En la misma recta numérica representamos el segundo intervalo (1,4) que empieza en -1 con un punto vacío y termina en 4 con otro punto vacío, al ser un intervalo abierto:

La intersección de intervalos es la parte común a los dos intervalos. En este caso, la parte común empieza en 1 y termina en 2.

El 1 está relleno por el primer intervalo, pero hay un punto vacío por el segundo intervalo, luego no es común a los dos y por tanto se queda abierto por la izquierda.

El 2 tiene un punto vacío por el primer intervalo y se queda relleno por el segundo intervalo. Como tampoco es común a los dos intervalos, queda abierto por la derecha.

La intersección de ambos intervalos nos queda entonces:

Intersección de intervalos separados

Vamos a ver cómo calcular la intersección de dos intervalos cuando estos se encuentran separados en la recta real.

Por ejemplo:

Representamos ambos intervalos en la recta real y nos queda:

En este caso, los intervalos no tienen ningún punto en común, luego la intersección de intervalos sería el conjunto vacío:

 INECUACIONES DE PRIMER Y SEGUNDO GRADO

INECUACIONES DE PRIMER GRADO

Una inecuación de primer grado es una desigualdad en la que la potencia de variable es uno.

Resolución de una inecuación de primer grado paso a paso

Hallar los valores de {x} que satisfacen la inecuación

 
1 Eliminamos primero los paréntesis y después los corchete 

2 Para eliminar los denominadores multiplicamos ambos lados de la inecuación por el mínimo común multiplo de los denominadores que aparecen en la inecuación, es decir, por {mcm(2,3,12)=12} y simplificamos las expresiones

3 Despejamos las {x} al lado izquierdo de la inecuación y las constantes al lado derecho. Para esto restamos {30} y {39x} en cada lado de la inecuación y simplificamos las expresiones

4 Para despejar {x} multiplicamos ambos lados de la inecuación por {-1/9}. Al multiplicar ambos lados por un número negativo, se cambia el sentido del símbolo de la inecuación

5 También podemos expresar la solución de la inecuación en forma gráfica

INECUACIONES DE SEGUNDO GRADO

Una inecuación de segundo grado o inecuación cuadrática es la que tiene la forma: ax2 + bx + c ≤ 0 , ( o ≥ 0, o > 0, o < 0) Siendo a > 0 siempre. 

Para resolverlas se hallan las dos raíces, tomada la expresión como una ecuación, x1 y x2 . Luego se factoriza el polinomio característico: (x - x1).( x - x2 ) ≤ 0 ó (x - x1).( x - x2 ) ≥ 0 Y por último se halla el signo de cada factor en cada uno de los siguientes intervalos: (-oo, x1), ( x1 , x2 ) y ( x2, +oo) La solución será un intervalo abierto o cerrado si las raíces halladas, x1 y x2 , pertenecen o no a la solución del sistema.

BIBLIOGRAFIA

Algebra (Significado) 

Operaciones aritmeticas con polinomios (Maths) 

Productos Notables (SuperProf)

Casos de Factorizacion (Juliosoria) 

Ecuaciones de Primer Grado y Segundo Grado (Superprof) 

Sistema de Ecuaciones con Dos Incognitas (YoSoyTuProfe) 

Sistema de Ecuaciones con Tres Incognitas (NeuroChispas) 

Intervalos (EnciclopediaEconomica) 

Operaciones con Intervalos (eafit) 

Union e Intersección (Ekuatio) 

Inecuaciones de Primer Grado (Superprof) 

Inecuaciones de Segundo Grado (SlidePlayer)