MATRICES

Las matrices son un conjunto bidimensional de números o símbolos distribuidos de forma rectangular, en líneas verticales y horizontales, de manera que sus elementos se organizan en filas y columnas. Sirven para describir sistemas de ecuaciones lineales o diferenciales, así como para representar una aplicación lineal.

Toda matriz se representa por medio de una letra mayúscula, y sus elementos se reúnen entre dos paréntesis o corchetes, en letra minúscula. A su vez, tienen doble superíndice: el primero hace referencia a la fila y el segundo a la columna a la que pertenece.

Esta expresión matemática puede sumarse, multiplicarse y descomponerse, por lo que su uso es común en el álgebra lineal.

 

 

 

 

 

 

 

 

 

 

 

 

 

MATRICES BOOLEANAS

Una matriz booleana es una matriz de números cuyas componentes o entradas son exclusivamente ceros o unos. Las matrices booleanas son útiles porque pueden representar objetos abstractos como relaciones binarias o grafos. 

Las operaciones que se pueden realizar entre matrices booleanas son tres: unión, conjunción y producto booleano. Sin embargo, estas operaciones no pueden realizarse sobre dos matrices cualesquiera, sino que deben cumplir ciertos criterios para poder llevarse a cabo. En particular, en el caso de la unión y la conjunción, las matrices que intervienen en la operación deben tener el mismo tamaño, y en el caso del producto booleano, las matrices deben cumplir con las mismas condiciones que para formar el producto de matrices. 

 

 

 

OPERACIONES: UNIÓN - INTERSECCIÓN

Unión / Disyunción

Sean A, B y C matrices booleanas de nxm elementos. Se define A ∨ B = C {\displaystyle A\vee B=C} la unión de A y B, por:

 

 

 

          Intersección / Conjunción

Sean A, B y C matrices booleanas de nxm elementos. Se define A ∧ B = C {\displaystyle A\land B=C} la intersección de A y B, por:

 

OPERACIÓN: PRODUCTO BOOLEANO

El producto booleano de las matrices A=[aij] y B=[bij], órdenes mxk  y  kxn respectivamente, se denotado por A O B. Este producto es la matriz mxn cuyo elemento (i,j ) es cij, donde: 

 

 

 

      POTENCIA BOOLEANA R-ESIMA

La potencia r-ésima de una matriz cuadrada A es el producto booleano de r (entero positivo) factores iguales. Esta potencia booleano r-ésima se denota por A[r].

 

 

LOGICA DE BITS (NOT, AND, OR, XOR)

https://learn.microsoft.com/es-es/dotnet/visual-basic/programming-guide/language-features/operators-and-expressions/logical-and-bitwise-operators

Los operadores lógicos comparan expresiones Boolean y devuelven un resultado Boolean. Los operadores And, Or, AndAlso, OrElse y Xor son binarios porque toman dos operandos, mientras que el operador Not es unario porque toma un único operando. Algunos de estos operadores también pueden realizar operaciones lógicas bit a bit en valores enteros.

NOT

Realiza una negación lógica en una expresión Boolean. Genera el opuesto lógico de su operando. Si la expresión se evalúa como True, Not devuelve False; si la expresión se evalúa como False, Not devuelve True.

AND

Realiza una conjunción lógica en dos expresiones Boolean. Si ambas expresiones se evalúan como True, And devuelve True. Si al menos una de las expresiones se evalúa como False, And devuelve False.

OR

Realiza una disyunción o inclusión lógica en dos expresiones Boolean. Si cualquiera de las expresiones se evalúa como True, o ambas se evalúan como True, Or devuelve True. Si ninguna expresión se evalúa como True, Or devuelve False.

XOR

Realiza una exclusión lógica en dos expresiones Boolean. Si exactamente una expresión se evalúa como True, pero no ambas, Xor devuelve True. Si ambas expresiones se evalúan como True, o ambas se evalúan como False, Xor devuelve False.

COMPUERTAS LOGICAS Y ALGEBRA DE BOOLE

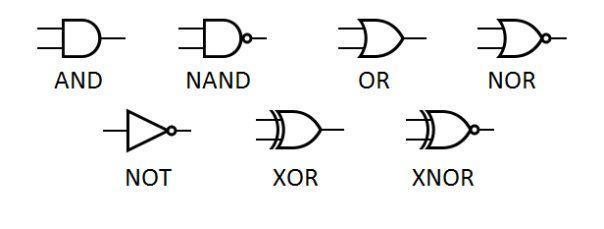
COMPUERTAS LOGICAS

Las Compuertas Lógicas son circuitos electrónicos conformados internamente por transistores que se encuentran con arreglos especiales con los que otorgan señales de voltaje como resultado o una salida de forma booleana, están obtenidos por operaciones lógicas binarias (suma, multiplicación). También niegan, afirman, incluyen o excluyen según sus propiedades lógicas. Estas compuertas se pueden aplicar en otras áreas de la ciencia como mecánica, hidráulica o neumática.

Existen diferentes tipos de compuertas y algunas de estas son más complejas, con la posibilidad de ser simuladas por compuertas más sencillas. Todas estas tienen tablas de verdad que explican los comportamientos en los resultados que otorga, dependiendo del valor booleano que tenga en cada una de sus entradas.

 

 

 

ALGEBRA DE BOOLE

El ALGEBRA DE BOOLE es un formalismo que conlleva a la creación de FUNCIONES LÓGICAS donde las mismas relacionan una variable binaria de salida con una o mas de entrada.
Dichas funciones se basan en una serie de postulados y teoremas que imponen las reglas de juego entre dichas variables.

 

 

 

MAPAS DE KARNAUGH

Un mapa de Karnaugh23 (también conocido como tabla de Karnaugh o diagrama de Veitch) es un diagrama utilizado para la simplificación de funciones algebraicas en forma canónica. A partir de la tabla de Karnaugh se puede obtener una forma canónica mínima (con el mínimo número de términos). En este texto emplearemos indistintamente los términos “mapa” y “tabla” de Karnaugh.

La tabla de Karnaugh consiste en una representación bidimensional de la función que se quiere simplificar. Si la función viene expresada como una tabla de verdad, entonces la tabla de Karnaugh puede verse como una forma alternativa de representación 2D. Puesto que la tabla de verdad de una función de n variables posee 2n filas, la tabla de Karnaugh correspondiente debe poseer también 2n celdas. La construcción de la tabla de Karnaugh pasa por codificar cada celda en código binario reflejado (o código Gray) de manera que celdas adyacentes tengan un código que difiere en un solo dígito.

 

 

 

GRAFOS DIRIGIDOS 

Dentro de los principales tipos de grafos que podemos estudiar están los grafos dirigidos.

Éstos son una especie de grafo que cuentan con elementos clásicos de un grafo simple pero con la particularidad de que sus aristas que conectan los nodos tienen una direccionalidad clara. Adicionalmente a los grafos dirigidos tenemos los que conocemos como grafos completos.

Un grafo completo de forma similar cumple con los requisitos de un grafo simple o dirigido. La diferencia que se presenta en este tipo de grafos es que cada par de nodos debe estar interconectado entre sí con diferentes conjuntos de aristas que conforman un camino.

Por su parte los grafos conexos son aquellos que cumplen con una condición especial. Para que un grafo se considere conexo entre los nodos que lo integran deben existir “caminos simples”. De esta estructuración de nodos nace lo que conocemos como árboles de grafos.

Sumado a esta clasificación tenemos los grafos etiquetados. A diferencia de los tipos de grafos anteriores, los grafos etiquetados incorporan datos en las aristas que le proporcionan peso a un grafo y estos son los más comunes en el mundo informático en el que vivimos.

      BIBLIOGRAFÍA 

           Matrices (Ferrovial) 

          Matriz Booleana (Wikipedia)

Producto Booleano (HikariHonda)

Potencia Booleana r-esima (Blogger)

          Grafos Dirigidos (Unican.es)

          Algebra de Boole (UNLP)

          Compuertas Logicas (LogicBus)